뉴럴 네트워크(Neural Network)
AI의 기본 구성 요소 중 하나로 매우 매우 복잡하게 이루어져 있다. 뉴럴 네트워크를 사용하는 경우의 중요한 문제 중 하나는 CPU는 물론 GPU에서도 네트워크의 트레이닝에 시간이 오래 걸린다는 것이다.
신경 네트워크는 Back Propagation 알고리즘을 사용하여 문제을 진행한다. 역전파(Back Propagation)를 통해 뉴런은 얼마나 많은 오차를 발생했는지를 학습하고 스스로 오차를 수정한다. 즉, "weights"와 "biases"를 수정한다. 이것에 의해, 입력이 주어졌을 때 올바른 출력을 생성하기 위해 문제를 학습한다. Back Propagation 에는 각 레이어의 구배를 계산하여 역방향으로 전파하는 작업이 포함되어 있다.
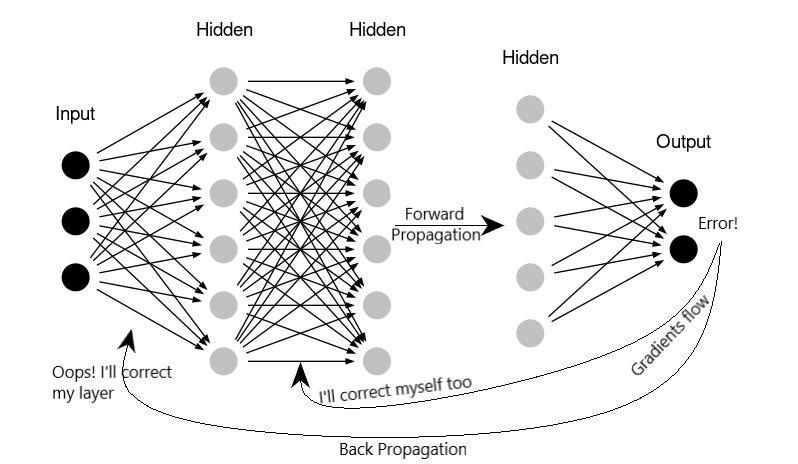
[The BackPropagation Algorithm]
하지만 "weights"와 "biases"에 대한 오차를 역전파하는 동안, 내부 공변량 이동이라는 원치 않는 특성에 직면하게 될 것이다.
이것에 의해, 네트워크가 너무 길어져 트레이닝할 수 없게 된다.
내부 공변량 이동(Internal Covariage Shift)
트레이닝 중에 각 레이어는 순전파(Forward Propagation) 중에 발생한 오류를 수정하려고 한다. 그러나 모든 계층은 개별적으로 작용하여 발생한 오류를 스스로 수정하려고 할 것이다.
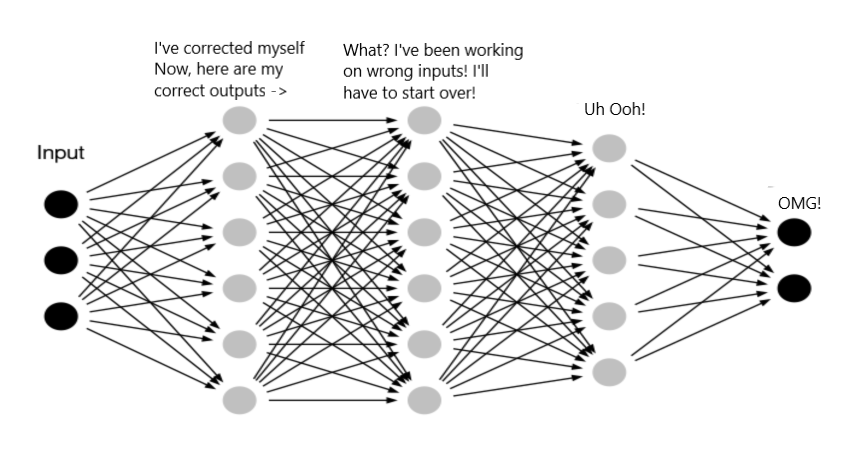
[Internal Covariate Shift]
예를 들어, 위의 네트워크에서는 두 번째 레이어가 weight와 biases를 조정하여 출력을 수정할 경우 이 조정에 의해 제2층의 출력, 즉 제3층의 입력이 같은 초기 입력으로 변경된다. 따라서 세 번째 계층은 동일한 데이터에 대한 올바른 출력을 생성하기 위해 처음부터 학습해야 한다.
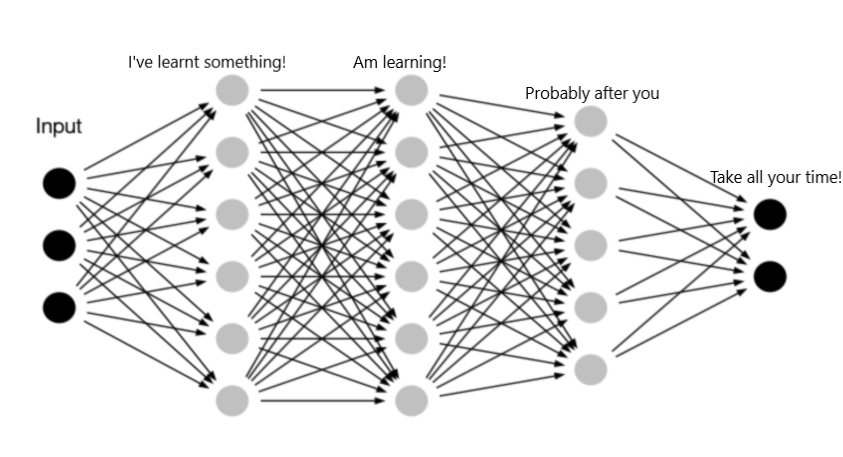
[Order of training]
위의 레이어는 이전의 레이어로부터 학습을 시작하는 문제를 나타내고 있다.
즉, 3번째 레이어는 2번째 레이어를 종료한 후에 학습을 시작하고, 4번째 레이어는 3번째 레이어 후에 학습을 시작되어 반복되는 작업을 거치게 된다. 만약 100~1000층 깊이의 심층 신경망을 생각해 보자.
이렇게 깊은 신경망을 훈련시키려면 정말 획기적인 것이 필요할 것이다.
보다 구체적으로, 이전 계층의 가중치의 변화로 인해, 현재의 계층에 대한 입력 값의 분포가 변화하여 새로운 "입력 분포(input distribution)"로부터 학습하도록 되어야 한다.
정규화(Normalization)
데이터 집합에서 모든 기능(열)이 동일한 범위에 있지 않을 수 있다. 예를 들면. 주택 가격, 주택 연령 등 이러한 종류의 데이터셋에 대해 교육하는 데 많은 시간이 걸린다.
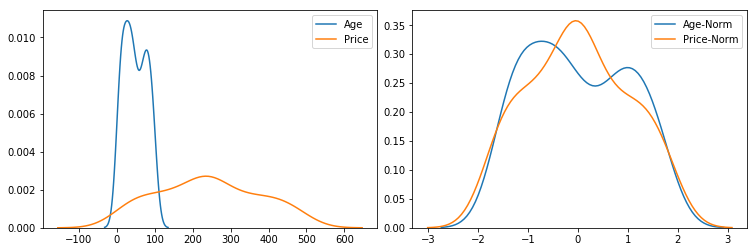
[Raw andnormalized data]
일반적으로 선형 회귀 분석과 같은 단순한 Machine Learning Algorithms에서는 입력을 단일 분포로 만들기 위해 훈련 전에 "정규화"한다. 정규화는 모든 입력의 분포를 평균 = 0 및 표준 편차 = 1로 변환하는 것이다. 따라서 대부분의 값은 -1과 1 사이에 있다.
이 정규화를 신경망의 입력에도 적용할 수 있다. 선형 회귀 분석과 같이 훈련을 빠르게 하게 되는데, 그러나 두 번째 계층은 이 분포를 변경하므로 연속되는 계층은 혜택을 받지 않는다.
그러면, 우리는 무엇을 할 수 있을까?
각 레이어 사이에 정규화를 추가하는 것은 어떨까? 이것이 Batch 정규화의 기능이다.
배치 정규화(Batch Normalization)
이러한 내부 공변량 이동 문제를 줄이기 위해 배치 정규화는 각 레이어 사이에 정규화 "레이어"를 추가하게 된다. 여기서 주목해야 할 중요한 것은 정규화는 모든 차원이 아닌 각 차원(입력 뉴런)에 대해 'mini-batches'에 걸쳐 개별적으로 이루어져야 한다는 것이다.

정규화는 완전히 연결된 각 레이어 간의 "레이어"로 인해 이전 레이어의 변경에 관계없이 각 레이어의 입력 분포 범위는 동일하게 유지된다.
k번째 뉴런에서 x개의 입력이 주어진다.

정규화는 0을 중심으로 하는 모든 입력을 가져온다. 이렇게 하면 각 레이어 입력에 큰 변화가 없을 것이다. 따라서 뉴럴 네트워크 내의 계층은 이전 계층이 학습할 때까지 기다리지 않고 동시에 역전파로부터 학습할 수 있다. 그래서 네트워크의 트레이닝이 고속화시킬 수 있다.
최고의 성능을 발휘하는 ImageNet 분류 네트워크에 Batch Normalization을 적용하여 트레이닝 스텝의 7%만으로 성능을 발휘하며, 정확성을 크게 웃도는 수준이다. — Original BatchNorm Paper
배치 정규화는 엄청난 효과를 불러오지만, BatchNorm에 대해 처리해야 할 몇 가지 문제가 있다.
Scale and Shift
일반적으로 Batch Normalization을 적용할 수 있는 유형은 아래와 같다.
- 활성화 기능 전(비선형성)
- 비선형성 후
원본 문서에서는 활성화 함수 적용 전에 BatchNorm이 적용되었다. 대부분의 활성화 함수 기능은 이러한 방식으로 적용하면 문제가 발생한다. Sigmoid 및 tanh 활성화 함수의 경우 정규화된 영역은 비선형이라기보다는 선형이다.
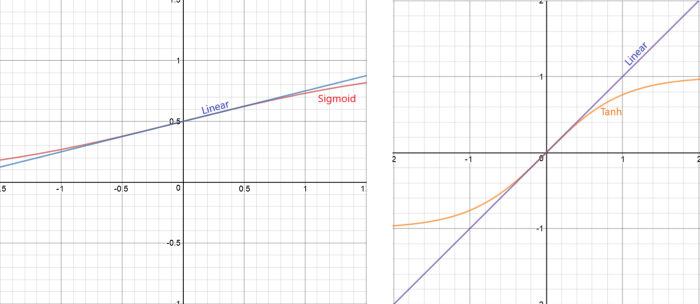
relu 활성화 함수의 경우 입력의 절반이 0이다.
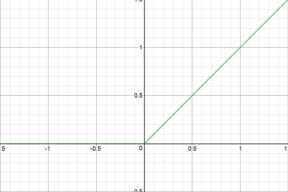
따라서, 분포를 0에서 멀리 이동하려면 변환해야 한다. 이를 위해 스케일링 계수 γ 및 시프트 계수 β 를 이용한다.
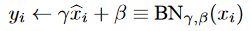
훈련이 진행됨에 따라 γ 와 β 도 역전파를 통해 학습하여 정확도를 향상한다. 따라서 학습 속도를 높이기 위해 각 레이어에 대해 2개의 추가 매개 변수를 학습해야 한다.
최근에는 활성화 함수 후 BatchNorm을 적용하면 성능이 향상되고 정확도도 향상되는 것이 관찰되고 있다.
이 경우 스케일링이나 시프트(Scale and Shift)는 하지 않고 BatchNorm 만 사용한다. γ = 1 및 β = 0으로 설정한다.
추론 시간의 BatchNorm
이제 배치 정규화가 학습 시간에 각 미니 배치의 평균과 분산을 계산하고 역전파를 사용하여 학습한다는 것을 알았다. 그런데 추론할 때는 어떻게 해야 할까? 미니 배치 테스트의 평균과 분산을 사용하면 왜곡될 수 있기 때문에 좋지 않을 것이다.
학습 후 모든 미니 배치 평균과 분산을 사용하여 평균과 분산의 "모집 평균"을 계산한 후 추론할 때 평균과 분산을 이 값으로 고정하고 정규화에 사용한다. 이것은 평균과 분산의 더 정확한 값을 제공하게 될 것이다.
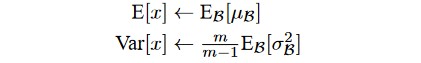
그러나 모든 미니 배치 평균과 분산을 추적하는 것은 어려울 수 있다. 이러한 경우 지수 가중치 "이동 평균"을 사용하여 모집단 평균과 분산을 업데이트할 수 있다.
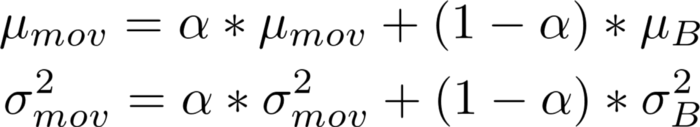
여기서 α 는 이전 이동 통계량에 주어진 "모멘텀"으로 약 0.9이다. 그리고 B는 mini-batch 평균과 mini-batch variance이다. 이는 대부분의 라이브러리에서 볼 수 있는 구현으로, 모멘텀을 수동으로 설정할 수 있다.
여기서 주의할 점은 이동 평균과 이동 분산은 테스트 시간이 아닌 학습 데이터셋을 사용하여 계산된다는 것이다.
BatchNorm에 의한 정규화
신경망의 학습 속도를 높일 뿐만 아니라, BatchNorm 은 또한 약한 형태의 정규화를 제공한다. 정규화는 데이터에 노이즈가 유입되어 발생할 수 있으며 전체 데이터셋에서 수행되는 것이 아니라 미니 배치에서만 수행되므로 노이즈로 작용한다.
BatchNorm 은 약한 정규화만 제공하므로 과적합을 방지하기 위해 완전히 의존해서는 안 된다.
하지만 그에 따라 다른 정규화는 줄어들 수 있다. 예를 들어 0.6(drop rate)의 드롭아웃을 지정할 경우 BatchNorm을 사용하면 drop rate를 0.4로 낮출 수 있다. BatchNorm 은 배치 크기가 작을 때만 정규화가 효율적이다.
이것으로 Batch Normalization에 대한 소개를 마무리하며, 다음 투고에서는 Tensorflow에서 배치 정규화 레이어를 어떻게 사용할 수 있는지 알아보자.
'인공지능' 카테고리의 다른 글
| [Part2]Sketch2Pokemon-Generator 구성하기|Pix2Pix (0) | 2022.03.23 |
|---|---|
| [Part1]Sketch2Pokemon-데이터 준비하기|Pix2Pix (0) | 2022.03.23 |
| [Tip]Colab 노트북 바로 열기|Github (0) | 2022.03.22 |
| [Part3]난 스케치 넌 채색을... |GAN-Pix2Pix (0) | 2022.03.18 |
| [Part2]난 스케치 넌 채색을... |TF2-GAN (0) | 2022.03.18 |
